CARA MENCARI KEMIRINGAN GARIS (GRADIEN)
“Gradien adalah
nilai yang menunjukkan kemiringan/kecondongan suatu garis lurus”.
Umumnya, gradien disimbolkan dengan huruf “m”. Gradien akan
menentukan seberapa miring suatu garis pada koordinat kartesius. Gradien suatu
garis dapat miring ke kanan, miring ke kiri, curam, ataupun landai, tergantung
dari nilai komponen x dan komponen y nya. Contoh macam-macam kemiringan
(gradien) pada garis lurus dapat kamu lihat melalui gambar di bawah ini:
“Garis yang
gradiennya positif akan miring ke kanan, sedangkan garis yang gradiennya
negatif akan miring ke kiri”.
Pada gambar nomor 1,
ternyata garisnya miring ke kanan, sehingga dapat diketahui kalau gradiennya
akan bernilai positif. Sementara itu, pada gambar nomor 4, garisnya miring ke
kiri, sehingga gradiennya akan bernilai negatif. Bagaimana dengan gambar nomor
2 dan 3?
Selanjutnya mari kita
bahas bagaimana cara menentukan gradien suatu garis.
Terdapat dua
cara untuk mencari nilai gradien suatu garis yang bisa kamu ketahui, yaitu:
I. Jika
diketahui bentuk persamaan garisnya
Secara umum,
bentuk persamaan garis lurus ada dua macam, sehingga cara untuk menentukan
gradiennya juga berbeda beda, tergantung dari bentuk persamaan garisnya.
a. Persamaan
garis y = mx + c
Pada
persamaan garis ini, gradien dapat dicari dengan mudah, Kenapa?
Karena gradiennya adalah koefisien dari variabel x itu
sendiri, yaitu m.
Contoh:
- Garis y
= 3x + 2, koefisien x adalah 3. Jadi, gradien garis tersebut adalah 3.
- Garis y
= -2x + 8, koefisien x adalah -2. Jadi, gradien garis tersebut adalah -2.
b. Persamaan
garis ax + by + c = 0
Jika
diketahui persamaan garis ax + by + c = 0, maka langkah pertama yang harus kamu
lakukan adalah ubah persamaan
garis tersebut ke bentuk y = mx + c, dengan m adalah
gradien garis tersebut. Di sini, kamu harus perhatikan tanda +/- dari
koefisien masing-masing variabelnya, ya. Soalnya, tanda +/- akan berubah ketika
kita pindah ruas persamaannya. Coba perhatikan contoh soal di bawah
ini.
Contoh:
1. Hitunglah
kemiringan (gradien) pada persamaan garis berikut:
a) 5x + 2y -
8 = 0
b) 2x - 3y =
7
Penyelesaian:
a)
Pertama-tama, kita ubah dulu persamaan 5x + 2y - 8 = 0 ke bentuk y = mx + c,
sehingga persamaannya menjadi,
5x + 2y - 8 = 0
2y = -5x + 8
Koefisien x
bernilai positif, yaitu 5, sehingga setelah kita pindah ruas ke kanan akan
bernilai negatif. Begitu juga dengan konstanta -8 yang berubah tanda menjadi 8
karena pindah ruas ke kanan. Selanjutnya, kita bagi kedua ruas dengan 2.
y = (-5/2)x + 4
Jadi,
gradien dari persamaan garis tersebut adalah -5/2.
Gimana? Kalian paham nggak sampai sini? Oke, supaya kalian semakin paham, coba kalian kerjakan contoh poin b.
II. Jika
diketahui dua titik yang dilalui garis
Jika
diketahui dua titik yang dilalui suatu garis lurus, misalnya (x1,y1)
dan (x2,y2), maka gradiennya dapat diperoleh dengan
rumus m = ∆y/∆x = (y2-y1)/(x2-x1).
Contoh soalnya seperti ini.
Contoh:
Perhatikan gambar berikut:
Gradien garis k pada
gambar adalah...
Penyelesaian:
Diketahui dua buah titik yang dilalui oleh garis k, yaitu (4,0) dan (0,6).
Misalnya kita pilih (x1,y1) = (4,0) dan (x2,y2)
= (0,6), gradien garis tersebut dapat dicari menggunakan rumus
m = ∆y/∆x = (y2-y1)/(x2-x1).
Jadi, gradien garis tersebut adalah -3/2. Di sini
kamu bebas untuk memilih titik mana yang jadi (x1,y1) dan
titik mana yang jadi (x2,y2) ya karena hasilnya akan sama
saja.
Itulah sedikit materi yang bisa saya sampaikan,
untuk lebih jelasnya silakan kalian pelajari buku paket Matematika kelas VIII
halaman 149 sampai dengan 156.
Untuk tugasnya silakan kalian kerjakan Ayo kita
Berlatih 4.3 halaman 157 nomor 1 sampai dengan nomor 3.
Jawaban bisa dikirim lewat WA ke nomor
081390587404 ( p Dri ) untuk kelas VIIIA dan VIIIB.
SELAMAT
MENGERJAKAN



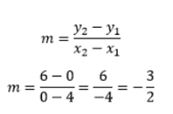
Tidak ada komentar:
Posting Komentar