MATEMATIKA KELAS 9| FUNGSI KUADRAT (1)

 

Fungsi kuadrat

 

Fungsi kuadrat adalah fungsi yang berbentuk y = ax² + bx + c, dengan a≠ 0,  x, y є R

Fungsi kuadrat dapat pula dituliskan sebagai f ( x ) = ax² + bx + c .

Bagaimanakah caramenggambar fungsi kuadrat pada bidang kartesius? Apa pengaruh nilai a, b, dan c terhadap grafik fungsi kuadrat?

 

Kegiatan 1. Menggambar grafik fungsi y = ax²

 

Menggambar grafik fungsi kuadrat yang paling sederhana, yakni ketika

b = c = 0.

Untuk mendapatkan grafiknya kamu dapat membuat gambar untuk beberapa nilai x dan mensubsitusikannya pada fungsi y = ax²,

Untuk mendapatkan grafik suatu fungsi kuadrat , kamu terlebih dahulu harus mendapatkan beberapa titik koordinat yang dilalui oleh fungsi kuadrat tersebut.

1.      Melengkapi tabel

 2.     Tempatkan titik-titik koordinat yang berada dalam tabel pada bidang koordinat(gunakan tiga                 warna  berbeda)

3.    Sketsa grafik dengan menghubungkan titik-titik koordinat tersebut

Ket :

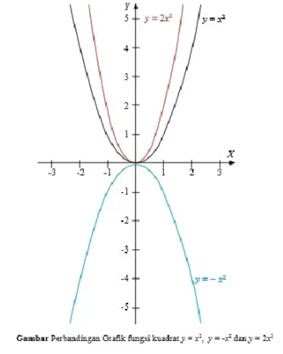
            Kurva y = x² ditandai dengan warna biru

            Kurva y = 2x² ditandai dengan warna hijau

            Kurva y = -2x² ditandai dengan warna merah

Nilai a pada fungsi y = ax² akan mempengaruhi bentuk grafiknya

§  Jika a ˃ 0, maka grafiknya akan terbuka ke atas

§  Jika a ˂ 0, maka grafiknya akan terbuka ke bawah

§  Jika a ˃ 0 dan nilai a semakin besar, maka grafiknya akan semakin “ kurus “

§  Jika a ˂ 0 dan nilai a semakin kecil, maka grafiknya akan semakin “ gemuk “

Kegiatan 2. Menggmbar grafik fungsi y = ax² + c

Kegiatan ini dibagi menjadi 2 sub kegiatan. Pada kegiatan ini kamu menggambargrafik fungsi   y = ax² + c sebanyak 3 kali, yakni untuk c = 0, c = 2, dan c = - 2

1.      Melengkapi tabel

              Untuk tabel y = x²  bisa kalian lihat pada tabel sebelumnya.

         2.    Tempatkan titik – titik koordinat yang berada pada tabel pada bidang koordinat Cartesius ( gunakan 3 warna berbeda )

          3.    Sketsa grafik dengan menghubungkan titik – titik koordinat tersebut.

Keterangan :

Kurva y = x² ditandai dengan warna biru

Kurva y = x² + 2  ditandai dengan warna coklat

Kurva y = x² – 2  ditandai dengan warna ungu

Berdasarkan hasil pengamatan dapat dilihat bahwa :

           1.      Grafik fungsi y = x² memotong sumbu Y di titik pangkal koordinat ( 0,0 )

           2.      Grafik fungsi y = x² + 2  memotong sumbu Y di titik koordinat ( 0,2 )

           3.      Grafik fungsi y = x² - 2  memotong sumbu Y di titik koordinat ( 0,-2 )

           4.      Grafik fungsi y = x² + 2  merupakan geseran grafik fungsi y = x² sepanjang 2 satuan ke atas

           5.      Grafik fungsi y = x² - 2  merupakan geseran grafik fungsi y = x² sepanjang 2 satuan ke bawah

            6.      Nilai c pada fungsi y = x² – c  akan mempengaruhi geseran grafik y = x², yaitu bergeser c satuan ke atas jika c > 0 dan  bergeser c satuan ke bawah jika c < 0

            7.      Grafik fungsi y = x² – c memotong sumbu – Y di titik koordinat (0,c)

 Kegiatan 3. Menggambar grafik fungsi y = x² + bx

Kegiatan ini akan menjadi tiga sub kegiatan, yakni ketika b = 2, b = -2. Pada kegiatan ini kamu akan mengenal titik puncak dari suatu grafik fungsi kuadrat.

1.    Melengkapi tabel di bawah ini

 2.    Tempatkan titik-titik koordinat yang berada dalam tabel pada bidang koordinat (gunakan tiga warna berbeda)

3.    Sketsa grafik dengan menghubungkan titik-titik koordinat tersebut

Ket :

Kurva y = x² + 2x ditandai dengan warna biru

Kurva y = x² – 2x  ditandai dengan warna hijau

Kurva y = -x² + 2x ditandai dengan warna merah

1.      Titik puncak adalah titik koordinat yang merupakan titik paling atas atau paling bawah

2.      Sumbu simetri adalah garis vertikal yang melalui titik puncak.

3.      Pengaruh nilai b pada grafik fungsi y = ax² + bx  adalah titik puncaknya berada di koordinat (x_p, y_p),

 Fungsi kuadrat merupakan fungsi yang berbentuk y = ax² + bx + c, dengan a≠ 0. Grafik dari fungsi kuadrat menyerupai parabola, sehingga dapat dikatakan juga sebagai fungsi parabola

Nilai a pada fungsi y = ax² + bx + c akan mempengaruhi bentuk grafiknya. Jika a positif maka grafiknya akan terbuka keatas. Sebaliknya jika a negatif maka grafiknya akan terbuka kebawah. Jika nilai a semakin besar maka grafiknya menjadi lebih “kurus”

Garis putus-putus pada gambar diatas merupakan sumbu simetri. Koordinat yang ditandai dengan bulatan merupakan titik puncak sedangkan koordinat yang ditandai dengan persegi merupakan titik potong dengan sumbu – Y

Nilai b pada grafik y = ax² + bx + c menunujukkan dimana koordinat titik puncak dan sumbu simetri berada (titik puncak dan sumbu simetri dibahas lebih lanjut pada sun-bab selanjutnya). Jika a > 0 maka grafiknya y = ax² + bx + c memiliki titik puncak minimum. Jika a < 0 maka grafik y = ax² + bx + c memiliki titik pucak maksimum.

Nilai c pada grafik y = ax² + bx + c menunjukkan titik perpotongan grafik fungsi kuadrat tersebut dengan sumbu – Y, yakni pada koordinat (c,0).

Berikut ini adalah grafik lima fungsi kuadrat yang berbeda.

         1.      grafik yang berwarna hitam merupakan grafik fungsi kuadrat y = x² – x + 2.

         Grafik y = x² – x + 2 memotong sumbu – Y pada koordinat (0,2) dan memiliki titik puncak minumum                     

         2.      Grafik yang berwarna merah merupakan grafik fungsi kuadrat y =2x² – 6x + 4.

         Grafik y =2x² – 6x + 4 memotong sumbu -Y pada koordinat (0,4) dan memiliki titik puncak minimum

         3.      Grafik yang berwarna biru merupakan grafik fungsi kuadrat y =-2x² + 8. Grafik

          y =-2x² + 8 memotong sumbu -Y pada koordinat (0,8) dan memiliki titik puncak maksimum

         4.      Grafik yang berwarna merah dengan garis putus-putus merupakan grafik fungsi kuadrat y =x² –7x + 10.Grafik y =x² – 7x + 10 memotong sumbu -Y pada koordinat (0,10) dan memiliki titik puncak minimum

         5.      Grafik yang berwarna bitu dengan garis putus-putus merupakan grafik fungsi kuadrat y = -x² – 5x - 6.Grafik y = -x² – 5x - 6 memotong sumbu -Y pada koordinat (0,-6) dan memiliki titik puncak maksimum

Ayo mencoba

Perhatikan persamaan di bawah ini dan selesaikan dengan menggunakan langkah-langkah pembuatan grafik yang telah dijelaskan sebelumnya !

Gambarlah grafik y = x² + x – 2

Penyelesaian:

1.      Lengkapi tabel

2.      Tempatkan titik-titik koordinat dalam tabel pada bidang koordinat

3.      Sketsa grafik dengan menghubungkan titik-titik koordinat tersebut

LATIHAN SOAL

Jawaban bisa dikirim lewat WA ke nomor 081390587404 ( p Driono )

Terimakasih.

SELAMAT MENGERJAKAN